12. 练习:最优策略
练习:最优策略
如果状态空间 \mathcal{S} 和动作空间 \mathcal{A} 是有限的,我们可以用表格表示最优动作值函数 q_*,每个可能的环境状态 s \in \mathcal{S} 和动作 a\in\mathcal{A} 对应一个策略。
特定状态动作对 s,a 的值是智能体从状态 s 开始并采取动作 a,然后遵守最优策略 \pi_* 所获得的预期回报。
我们在下方为虚拟马尔可夫决策流程 (MDP) (where \mathcal{S}={ s_1, s_2, s_3 } 和 \mathcal{A}={a_1, a_2, a_3}) 填充了一些值。

你在上一部分了解到,智能体确定最优动作值函数 q_ 后,它可以为所有 s\in\mathcal{S} 设置 \pi_(s) = \arg\max_{a\in\mathcal{A}(s)} q_(s,a) 快速获得最优策略 \pi_。
要了解为何是这种情况,注意,必须确保 v_(s) = \max_{a\in\mathcal{A}(s)} q_(s,a)。
如果在某个状态 s\in\mathcal{S} 中,有多个动作 a\in\mathcal{A}(s) 可以最大化最优动作值函数,你可以通过向任何(最大化)状态分配任意大小的概率构建一个最优策略。只需确保根据该策略给不会最大化动作值函数的动作(对于特定状态)分配的概率是 0% 即可。
为了构建最优策略,我们可以先在每行(或每个状态)中选择最大化动作值函数的项。
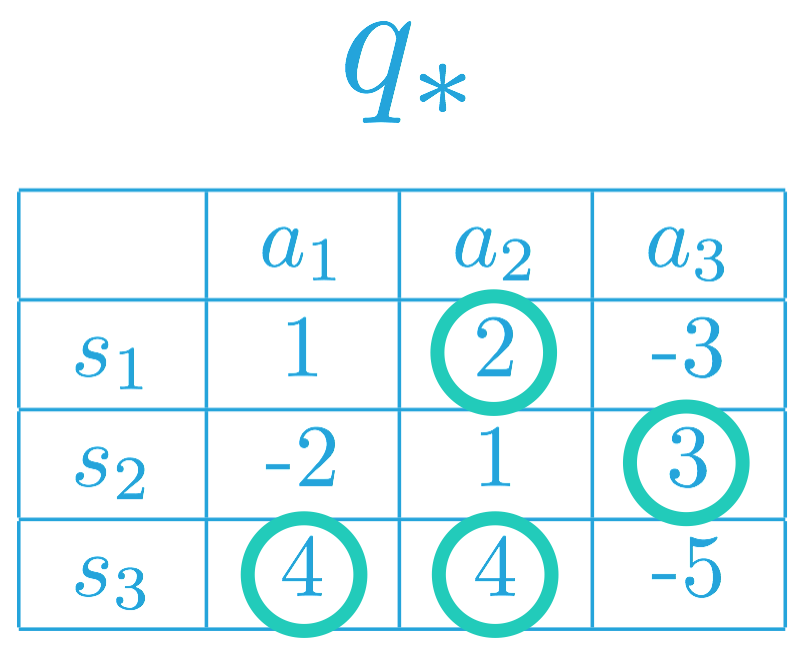
因此,相应 MDP 的最优策略 \pi_* 必须满足:
- \pi_(s_1) = a_2 (or, equivalently, \pi_(a_2| s_1) = 1),以及
- \pi_(s_2) = a_3 (or, equivalently, \pi_(a_3| s_2) = 1)。
这是因为 a_2 = \arg\max_{a\in\mathcal{A}(s_1)}q_(s,a),以及 a_3 = \arg\max_{a\in\mathcal{A}(s_2)}q_(s,a)。
换句话说,在最优策略下,智能体在状态 s_1 下必须选择动作 a_2,在状态 s_2 下将选择动作 a_3。
对于状态 s_3,注意 a_1, a_2 \in \arg\max_{a\in\mathcal{A}(s_3)}q_(s,a)。因此,智能体可以根据最优策略选择动作 a_1 或 a_2,但是始终不能选择动作 a_3。即最优策略 \pi_ 必须满足:
- \pi_*(a_1| s_3) = p,
- \pi_*(a_2| s_3) = q,以及
- \pi_*(a_3| s_3) = 0,
其中 p,q\geq 0 以及 p + q = 1。
问题
思考另一个对应不同的最优动作值函数的不同 MDP。请使用该动作值函数回答以下问题。
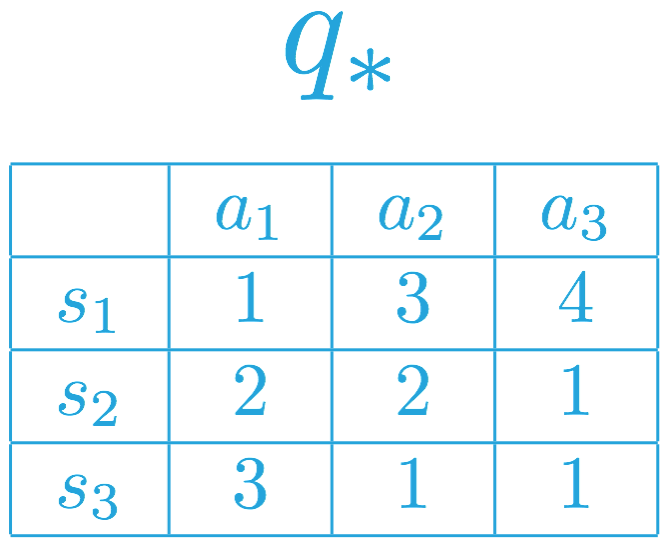
SOLUTION:
- 智能体在状态 s_1 始终选择动作 a_3。
- 智能体在状态 s_2 可以随意选择动作 a_1 或动作 a_2。
- 智能体在状态 s_3 必须选择动作 a_1。